1.1.Introduction
Souvent les problèmes nécessitent l'étude de plusieurs situations qui ne peuvent pas être traitées par les séquences d'actions simples. Puisqu'on a plusieurs situations, et qu'avant l'exécution, on ne sait pas à quel cas de figure on aura à exécuter, dans l'algorithme on doit prévoir tous les cas possibles.
Ce sont les structures conditionnelles qui le permettent, en se basant sur ce qu'on appelle prédicat ou condition.
1.2. Notion de PREDICAT
Un prédicat est un énoncé ou proposition qui peut être vrai ou faux selon ce qu'on est entrain de parler.
En mathématiques, c'est une expression contenant une ou plusieurs variables et qui est susceptible de devenir une proposition vraie ou fausse selon les valeurs attribuées à ces variables.
Exemple :
(10 < 15) est un prédicat vrai
(10 < 3) est un prédicat faux
1.3. Evaluation d'une expression logique
Une condition est une expression de type logique. Ils lui correspondent deux valeurs possibles VRAI et FAUX qu'on note par V ou F.
Considérons deux variables logiques A et B. Voyons quels sont les opérateurs logiques et leurs ordres de priorités.
1-a) Notons que
- (A = faux) <=> non A
- (A = vrai) <=> A
Les opérateurs logiques sont :
- La négation : "non"
- L'intersection : "et"
- L'union : "ou"
1-b) Notation et Ordre de priorité des opérateurs logiques
1. non : ¬
2. et : ^
3. ou : v
1-c)
1-d) Tableaux d'évaluations
La négation d'une condition
A
|
Non A
|
Vrai
|
Faux
|
Faux
|
Vrai
|
L'intersection de deux conditions
A et B
|
Vrai
|
Faux
|
| Vrai | Vrai | Faux |
| Faux | Faux | Faux |
L'union de deux conditions
| A ou B | Vrai | Faux |
| Vrai | Vrai | Vrai |
| Faux | Vrai | Faux |
Théorème de DE MORGAN
- ¬(A ^ B) ↔ ¬A v ¬B
- ¬(A v B) ↔ ¬A ^ ¬B
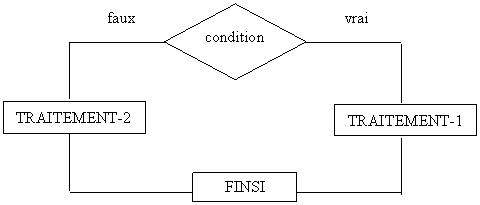
1.4. La structure conditionnelle SI
Syntaxe
SI <Condition> ALORS
<suite d’action(s)-1>
[SINON
<suite d’actions(s)-2>]
FINSI
Format Organigramme
·
La <condition> est un prédicat, qui peut être vrai ou faux, selon les valeurs des paramètres la constituant.
· Si la condition est vérifiée (sa valeur est vrai), c'est la <suite d'actions-1> qui sera exécutée. Ensuite, le système passe à l'exécution juste après le FINSI.
· Dans le cas contraire, lorsque la condition n'est pas vérifiée (valeur de la condition est faux), c'est la <suite d'actions-2> qui s'exécute, en cas où celle ci existe (facultative). Si elle n'existe pas, le système passe directement à l'instruction qui suit le FINSI.
· Les suites d'actions 1 et 2, peuvent être des actions simples ou même des structures conditionnelles.
1-e) Exemple 1
Lire un nombre réel, et dire s'il est positif ou strictement négatif.
ALGORITHME POS-NEG
VAR A : réel
DEBUT
ECRIRE("Donner un nombre ")
LIRE(A)
SI (A < 0) ALORS
ECRIRE(A, " est négatif ")
SINON
ECRIRE(A, " est positif ")
FINSI
FIN
Autrement :
ALGORITHME POS-NEG-1
VAR A : réel
B : logique
DEBUT
ECRIRE("Donner un nombre ")
LIRE(A)
B ¬ (A < 0)
SI (B) ALORS
ECRIRE(A, " est négatif ")
SINON
ECRIRE(A, " est positif ")
FINSI
FIN
Dans cet exemple, on a déterminé uniquement les cas de positivité ou de négativité, et on n'a pas déterminé le cas où A est nulle.
ALGORITHME POS-NEG-NUL
VAR A : réel
DEBUT
ECRIRE("Donner un nombre ")
LIRE(A)
SI (A < 0) ALORS
ECRIRE(A, " est négatif ")
SINON {A >= 0}
SI (A > 0)ALORS
ECRIRE(A, " est positif ")
SINON {A = 0}
ECRIRE (A, "est nulle")
FINSI
FINSI
FIN
1-f) Exemples
1) Ecrire l'algorithme qui permet de déterminer si un entier lu est pair ou impair.
2) Ecrire l'algorithme qui permet de saisir deux nombres A et B et de déterminer si la valeur de A est supérieure, inférieure ou égale à B.
1.5. La structure conditionnelle SELON
Cette structure conditionnelle est appelée aussi à choix multiple ou sélective car elle sélectionne entre plusieurs choix à la fois, et non entre deux choix alternatifs (le cas de la structure SI).
Syntaxe
SELON (sélecteur) FAIRE
Cas <liste de valeurs-1> : <suite d'action (s)-1>
[Cas <liste de valeur-2> : <suite d'action (s)-2>
………. ]
[SINON : <suite d'action (s)-n> ]
FINSELON
Le sélecteur peut être une variable de type scalaire ou une expression arithmétique ou logique.
La structure SELON évalue le "sélecteur", passe à comparer celui ci respectivement avec les valeurs dans les listes. En cas d'égalité avec une valeur, les actions correspondantes, qui sont devant cette valeur seront exécutées.
Devant "Cas", il peut y avoir une seule valeur, une suite de valeurs séparées par des virgules et/ou un intervalle de valeurs.
Après avoir traiter la suite d'actions correspondante, l'exécution se poursuit après le FINSELON.
Remarque
1. Le sélecteur doit avoir le même type que les valeurs devant les cas.
2. Le type de ces valeurs ne doit être, ni réel ni chaîne de caractères.
1-g) Exemple
Ecrire l'algorithme qui permet de saisir un numéro de couleur de l'arc-en-ciel et d'afficher la couleur correspondante : 1: rouge, 2 : orangé, 3 : jaune, 4 : vert, 5 : bleu, 6 : indigo et 7 : violet.